Extraits
de "L'Analyse Technique"
de Thierry Béchu, Eric Bertrand et Julien Nebenzalh
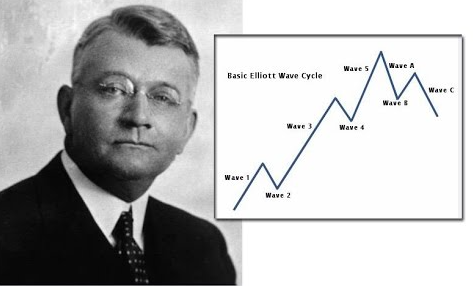
Ralph Nelson Elliott et le nombre d'or
Ralph Nelson Elliott (1871-1948) est un fervent croyant : qui ne comprend pas l’ordre, a priori divin, qui régit le monde pendant la grande dépression des années 30. Passionné de bourse, il a lu les ouvrages des disciples de Dow et trouve dans l’allégorie des « vagues » la seule vision qui permette de concilier la détresse des hommes (à cette époque, 40% des Américains vivent bien en dessous du seuil de pauvreté) et le principe du cycle boursier (la baisse de 90% de la bourse a précédé la Grande Dépression). D'une croyance à l’autre, Elliott dira que les impulsions haussière sont composées de cinq vagues tandis que les corrections trois.
Divina Proportione
Selon Kant, la croyance est le juste « milieu entre l'opinion et le savoir » ; Elliott, lui, va plus loin et qualifie de rythme « naturel » le lien entre toutes les vagues : qu'il s'agisse de leur durée ou de leur taille, tout est proportionné. De là, la fameuse « proportion dorée» suivie de nos jours, au travers des « ratios de Fibonacci » par de si nombreuses salles de marchés...
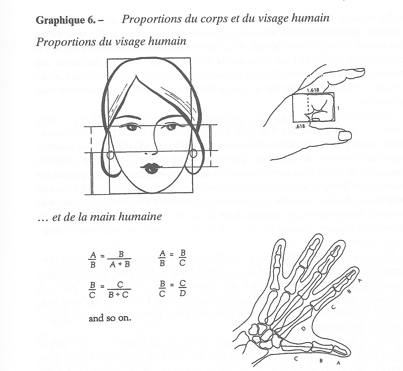Proporstion & Perfection
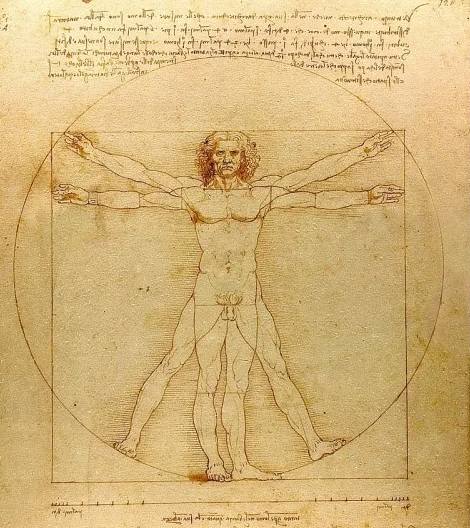L’Homme de Vitruve
1,61803398875...
Ce nombre fascine depuis très longtemps. Il suffit de taper "golden mean" sur Google pour être frappé
par la diversité des sites qui se l'approprient. On le voit partout, dans la philosophie, la
spiritualité, l'art, l'économie et... dans le trading!
Léonard de Vinci était fasciné par le corps humain et les mécanismes physiques qu’il contient mais
aussi bien dans l’esprit de Vitruve que dans celui de Vinci, cette représentation de l’homme est
purement artistique, pas du tout scientifique.
En reprenant ce dessin à son compte, Léonard de Vinci a souligné l’influence évidente de la géométrie
dans la création artistique,
et notamment le nombre d'or résultant des ratios de Fibonacci.
Anticipation
Il n'y a plus besoin d'attendre que les prix indiquent leur évolution prévisible puisque toute cette
évolution est déjà déterminée!
Avec Elliott, la frontière avec l’astrologie pourra désormais sembler franchie ; d'ailleurs, William
F. Eng publie en 1988 une
synthèse des connaissances en analyse technique (The technical
analysis of stocks, options and futures) en y incluant notamment l’astrologie,
«la meilleure conseillère quand il s’agit de déterminer à l’avance le point haut ou le point bas d'un
marché» dira l’auteur, qui ajoute que seules
l’astrologie, la théorie d'Elliott et celle de Gann permettent d’anticiper le changement de tendance.
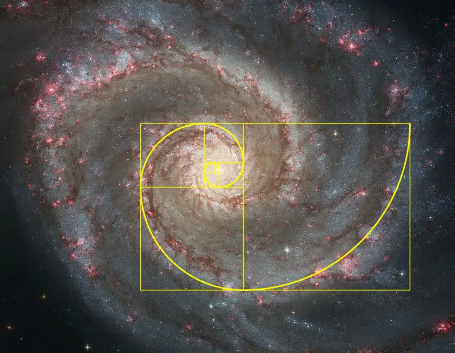Les spirales galactiques suivent le principe de la spirale de
Fibonacci
Elliott's Waves pattern
L'analyse technique philosophique peut exister à travers plusieurs théories qui proposent une interprétation globale des marchés. Ces théories sont établies sur des bases précises et permettent de comprendre tous les mouvements. Leur application offre la possibilité d'anticiper les variations à venir.
Les théories les plus répandues ont été développées par des hommes d’un certain génie et portent très souvent leur nom, comme c'est le cas pour Gann et Elliott. D'autres analyses appartiennent à ce registre des théories complexes, notamment celles qui considèrent que les marchés sont influencés par des éléments extérieurs comme l'astrologie. L'analyse astrologique des marchés a fait beaucoup de progrès ces dernières années, tout particulièrement grâce à l’ordinateur. Des programmes assez sophistiqués permettent en effet de superposer les variations de cours et les positions des planètes et d’en déduire une relation statistique. Les événements les plus suivis (pleine lune, changements de lune, éclipses de la lune et du soleil...) mettent ainsi en évidence des relations parfois étonnantes avec certains marchés.
Mais revenons à la théorie des Vagues d'Elliott.
Cette dernière représente la théorie la plus complète et la mieux élaborée. Par ailleurs, elle repose
sur une vision philosophique
de la vie et de l'univers. La théorie suppose en effet l’existence d'un certain équilibre universel que
l’on retrouve dans les manifestations
humaines des marchés financiers.
La théorie d'Elliott est également la théorie la plus travaillée et la plus suivie.
Elle offre par ailleurs l'avantage d’intégrer certains éléments de l’analyse technique traditionnelle.
De ce fait, cette théorie peut même être considérée comme une théorie enveloppante de l’analyse
technique.
R. N. Elliott s market letters
Les origines de la théorie des vagues d'Elliott
Fros Frechter
Aux États-Unis, la théorie d’Elliott - développée pendant les années 1930 - est désormais presqu'aussi célèbre et appréciée que l'analyse technique traditionnelle. Elle le doit beaucoup à Robert Prechter qui lui a permis de sortir de l’oubli dans lequel elle était tombée pendant plus de trente ans. Prechter s’est plongé dans cette théorie et lui a redonné vie. La publication en 1978 de son fameux livre écrit en collaboration avec A.J. Prost, The Elliott Waves Principle et surtout la qualité et la justesse de ses analyses publiées dans la revue The Elliott Wave Theorist ont permis aux vagues d’Elliott d’atteindre un niveau de célébrité étonnant et d’être pratiquées par un nombre croissant de traders sur les marchés de contrats à terme.
Pourtant, Ralph Nelson Elliott (1871-1948) avait connu en son temps les pires difficultés pour faire
publier ses travaux et les faire reconnaître.
R.N. Elliott fut comptable dans plusieurs compagnies de chemin de fer basées en Amérique centrale et au
Mexique.
Suite à une maladie contractée au Guatemala et à une certaine anémie, il mit fin à sa carrière en 1927 et
consacra alors son temps à recouvrer
une partie de sa santé et à étudier le comportement des marchés boursiers à travers les évolutions de
l’indice Dow Jones.
Ses travaux connurent deux influences bien différentes. Tout d’abord, il approfondit certains principes
que Charles Dow n’avait qu’esquissés.
Chez les deux hommes, la psychologie humaine est ainsi déterminante pour comprendre l’évolution des
marchés (mais Elliott va plus loin dans son analyse).
Leonardo Fibonacci
Le second guide d’Elliott est plus inattendu et plus éloigné dans le temps puisqu'il s’agit de Leonardo Fibonacci, mathématicien du XIIIe siècle, auquel Elliott va reprendre une partie de ces conclusions concernant le nombre d’or et la fameuse série de Fibonacci. L’intuition d’Elliott est assez étonnante : il suppose, en effet, que les fluctuations des marchés sont le reflet d’une somme de réactions psychologiques individuelles (Dow) et doivent refléter une harmonie fondamentale de la nature (Fibonacci). Selon lui, les marchés doivent fluctuer en respectant une harmonie naturelle, telle qu'on peut la retrouver dans la plupart des manifestations découvertes par Fibonacci. Les marchés doivent ainsi varier en suivant une certaine perfection ordonnée par la nature et l'harmonie universelle.
À partir de la série mathématique et des ratios de Fibonacci et après une étude pointilleuse de l’évolution du Dow Jones, Elliott est parvenu à déduire un ensemble de principes et de règles qui fondent sa théorie. Après un premier contact avec son éditeur en 1934, ce n'est qu’en 1938 qu’Elliott publiera The Wave Principle après avoir convaincu ce dernier de la qualité prédictive de sa théorie. Elliott publiera ensuite une série de 12 articles pour le Financial World Magazine en 1939 puis, en 1946, il écrira l’ouvrage définitif sur la théorie des vagues : Nature’s Law - The Secret of the Universe.
Nature’s Law
0,1,1,2,3,5,8,13,21,34,55,89,144...
Avant de découvrir les secrets de cette théorie, revenons sur les découvertes de Fibonacci.
En mathématiques, la suite de Fibonacci est une suite de nombres entiers dont chaque terme successif
représente la somme des deux termes précédents,
et qui commence par 0 puis 1. Ainsi, les dix premiers termes qui la composent sont 0, 1, 1, 2, 3, 5, 8,
13, 21 et 34.
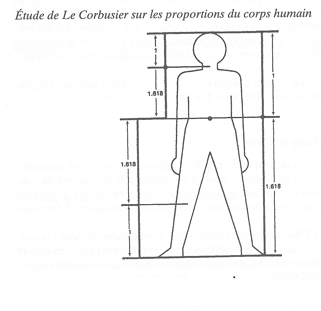Etude de Le Corbusier
Mais si cette suite est aussi célèbre aujourd’hui, c’est parce qu’elle a un taux de croissance exponentiel qui tend vers le nombre d’or, un ratio symbolisé par « φ » (Phi), qui permet de répondre à l’équation x²=x+1, et qui est associé à de nombreuses qualités esthétiques au sein de la civilisation, dans la nature et dans l'univers. Sa valeur exacte est de (1+√5)/2, ayant comme dix premières décimales 1,6180339887… Ce rapport, considéré comme la clé de l’harmonie universelle, se décline et se transpose par des formes géométriques telles que le rectangle, le pentagone, le triangle ou la spirale.
Pour constater à quel point le ratio de Fibonacci est partout présent dans la nature, pennons la longueur
réelle en km (A) de quelques cours d’eau de France:
la Loire, le Rhône, la Garonne, la Marne, le Lot, le Doubs et l’Oise puis on mesure la longueur à vol
d’oiseau de chaque cours d’eau choisi (B),
en tenant compte de l’échelle de la carte.
Maintenant divisons simplement la longueur réelle de chaque cours d’eau par sa longueur à vol d’oiseau.
On obtient :
| Fleuve | Valeur A | Valeur B | A / B |
|---|---|---|---|
| La Loire | 1020 km | 630 km | 1,619… |
| Le Rhône | 812 km | 502 km | 1,617… |
| La Garonne | 650 km | 402 km | 1,616… |
| La Marne | 525 km | 325 km | 1,615… |
| Le Lot | 480 km | 297 km | 1,616… |
| Le Doubs | 430 km | 266 km | 1,616… |
| L’Oise | 302 km | 180 km | 1,667… |
Le rapport entre la longueur réelle d’un cours d’eau et sa longueur à vol d’oiseau correspond approximativement au nombre d’or ou la divine proportion. Cette loi fut découverte par Albert Einstein et constatée par Hans-Hendrick Stolum, spécialiste des sciences de la Terre.
"Dieu a créé toute chose sur terre, y compris les nombres"
Leonardo de Pise, ou Fibonacci, né à Pise vers 1170 et mort après 1250 est considéré comme le plus grand mathématicien de tout le Moyen Âge chrétien. Très jeune, Léonard part avec son père à Béjaïa, en Algérie. Il y apprend l’arithmétique et la langue arabe et acquiert le goût des mathématiques. À son retour, il écrit son célèbre Liber Abaci (Le livre du calcul)i publié en 1202. Il s’agit d’une véritable encyclopédie qui va initier les savants italiens du XIIIe siècle à la science mathématique des Arabes et des Grecs et permettre à plus long terme les progrès de l’algèbre dans l’Italie de la Renaissance.
Liber Abaci
Le Liber Abaci s’ouvre sur les neuf symboles indiens de numération ainsi que sur le signe du zéro. Il y
traite entre autres de la résolution d’équations
du second degré, d’équations indéterminées, de calculs à effectuer avec des radicaux...
Il posa ainsi les jalons d’importants développements en mathématique, en physique et en astronomie.
Dans son Liber Abaci, Fibonacci traite d'un des problèmes les plus connus, à l'origine de
la découverte du nombre d'or :
Si un couple de lapins était installé sur une île déserte,
combien de paires de lapins y aurait-il au bout d’un an sachant que tous les mois une paire de lapins
produit une autre paire
qui commence à être « opérationnelle » deux mois après sa naissance ?
Partons donc d’un couple de lapins le premier mois. Le deuxième mois, il n’y a toujours que ce même couple qui est « opérationnel », mais le troisième mois il y a déjà 2 couples, puis 3 couples le quatrième mois, 5 couples le cinquième mois, etc. La croissance de cette population est bel et bien décrite par la suite de Fibonacci: 1 ; 1 ; 2 ; 3 ; 5 ; 8 ; 13 ; 21 ; 34 ; 55 ; 89 ; 144 ; 233 ; 377 ; 610 ; 987 et dont le dominateur commun est le nombre d'or 1,6180339887… .
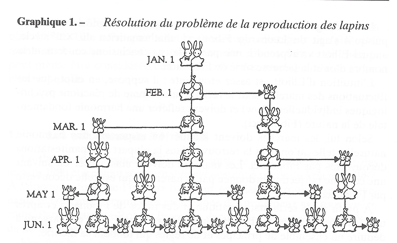Etude sur la reproduction des lapins
La série de Fibonacci dispose encore de bien d'autres propriétés, mais le plus important réside dans celles, beaucoup plus troublantes, du nombre d’or et du ratio d'or (1,618 et 0,618). Dans le Smithsonian Magazine de décembre 1975, William Hoffer notait les points suivants : " Le nombre d'or fait incontestablement partie d'une harmonie naturelle mystique et universelle. En musique, par exemple, l'octave est basé sur 8 notes. Au piano, cela est représenté par 8 touches blanches et 5 noires soit 13 en tout. Ce n'est pas un hasard si les meilleures harmonies musicales répondent à la règle du ratio d'or. "
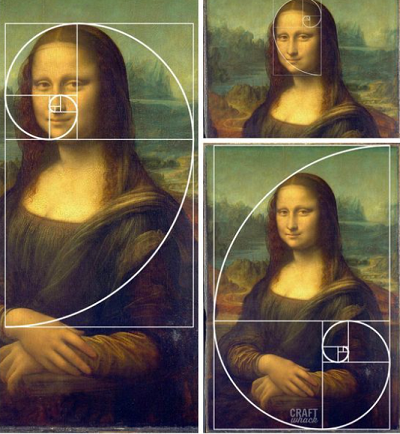Ratio de Fibonacci dans La Joconde
Ainsi l'homme recherche-t-il ce ratio pour obtenir une certaine harmonie? Léonard de Vinci était par exemple un adepte de ce nombre qu’il utilisait très souvent dans ses œuvres. Beaucoup d’autres artistes utilisent ce ratio d’or dans la composition de leurs tableaux ou de leurs photographies.
L'architecture utilise beaucoup ce ratio afin d’aboutir à des proportions esthétiques considérées comme idéales. La structure du Parthénon est un exemple parfait ou encore la grande pyramide de Giseh dont la longueur est égale à 1.618 multiplié par la moitié de sa base, de sorte que la hauteur de la pyramide est égale à la racine carrée de 1.618 multiplié par la moitié de sa base.
La structure du Parthénon
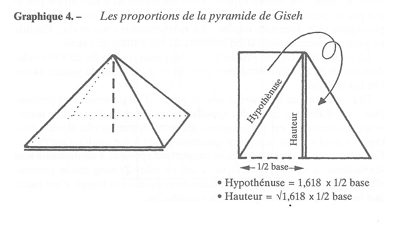La pyramide de Giseh
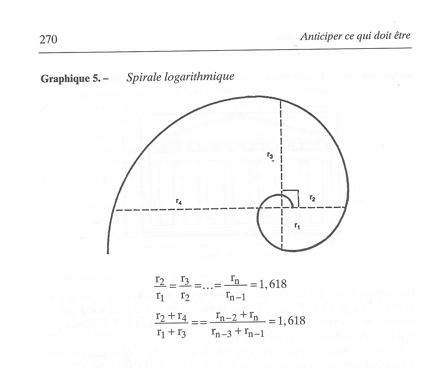Spirale logarithmique & nombre d’or
La spirale logarithmique que l’on retrouve aussi bien dans une coquille d’escargot que dans une galaxie en spirale et qui peut s’enrouler à l’infini est régie par le nombre d’or. En effet, chaque rayon est égal à 1,618 fois le rayon qui le précède d’un angle à 90°. Le nombre d’or a encore d’autres propriétés, mais celles que nous venons de détailler suffisent déjà pour apprécier l'importance de ce nombre tant dans notre vie de tous les jours que dans l'univers le plus lointain.
Inspiré par cette omniprésence universelle de ce nombre et des autres ratios de la série, N.R. Elliott en
a conclu que les cours de bourse devaient
également être entretenus par ce véritable mystère de la nature. Il restait - simplement - à en découvrir
la formule et les règles.
Elliott y consacra en tout près de vingt ans de sa vie et nous a légué une véritable théorie pratique de
l’influence des nombres de Fibonacci
sur l’évolution des marchés financiers, tout en conservant une vision très pragmatique basée sur la
psychologie des intervenants.
Je vous invite à vous inscrire pour découvrir la deuxième partie de l'article qui traite de la
présentation de la théorie d'Elliott et des façons de l'utiliser dans votre
Trading de tous les jours.
